Mínimos cuadrados

En la siguiente tabla tenemos los índices de productividad de la industria manufacturera de México, de 1988 a 1995.

Este índice representa cuánto produce un trabajador de la industria manufacturera, y como es claro de los datos, se ha incrementado año con año. Este aumento se debe, entre otros factores, al uso de mejores tecnologías en la industria manufacturera y a la mejor capacitación de los trabajadores. El objetivo de estos índices es comparar la productividad en diferentes años; para su elaboración el INEGI tomó como año base a 1993 y le asignó una productividad de 100. Así podemos ver que, por ejemplo de 1993 a 1994 la productividad aumento en 6.3 %. De continuar esta tendencia en aumento en la productividad, ¿Cuándo esperamos que la productividad sea 25% mayor que en 1993, es decir, que la productividad sea 125?y ¿cuál será la productividad en el año 2020?

Esta clase de preguntas equivale a expresar la productividad en términos del tiempo, es decir, si podemos expresar a la productividad como una función del tiempo. Recordemos que una función es una regla que asocia a un número otro número. Por ejemplo, la función f(x)= 0.5 x +1 asocia al número 2 el número 0.5 x 2 +1 = 2, al número 4 el número 0.5 x 4 +1 =3, al número 2/3 el número 0.5(2/3) +1 = 4/3, etc., o bien, la función $g (x)= x^2 - 0.5$ asocia al número 1 el número $1^2 – 0.5 = 0.5$; al número -2 el número $(-2)^2 - 0.5 = 3.5$ , etc. Recordemos también que una función puede ser descrita geométricamente por medio de su grafica. La grafica de una función es una recta o una curva en el plano. Las rectas corresponden a graficas de funciones lineales, es decir, donde a cada número x se le asocia el numero mx +b, como el caso de la función f. La grafica de la función f consiste en todos los puntos (x,y) del plano tales que y =0.5 x + 1, y como ya mencionamos, debe ser una recta, mientras que a grafica de la función g consiste en todos los puntos (x, y) del plano tales que $y = x^2 -0.5$ , y es una parábola. En las siguientes figuras tenemos estas graficas.

Gráfica de f (x) = 0.5 x +1

 

Gráfica de g (x) = $x^2 - 0.5$

Volvamos a las preguntas sobre la productividad de la industria manufacturera. Deseamos establecer alguna relación entre los años y el índice de productividad. Puesto que deseamos que esta relación se exprese lo más sencillo posible, es conveniente asignar al año 1988 el valor x= 0, al año 1989 el valor x = 1, así hasta el año 1995, que le asignamos el valor x =7. Grafiquemos ahora en el plano los puntos (0,88.5), (1, 91.5), (2, 94.4),… , (7, 106.3 ):

Una forma de responder a las preguntas sobre la productividad de la industria manufacturera consiste en averiguar si estos puntos pertenecen a la grafica de una función. Debido a la variedad de factores que intervienen en determinar  la productividad, nos basta con encontrar una función que pase por estos puntos. En este caso podríamos encontrar una recta que pase cerca de todos estos puntos, como la siguiente figura:

En este y el próximo post vernos como asociar a un conjunto de puntos del plano la recta que pasa más cerca de ellos. Esto nos permite establecer relaciones lineales entre dos tipos de variables, como puede ser los años y la productividad. Cabe señalar que aun cuando este método es sencillo, no siembre es conveniente usarlo  para expresar linealmente una variable en términos de otra. Por ejemplo, en la siguiente figura aparece el porcentaje de mujeres de 35 a 39 años por número de hijos nacidos vivos.

Porcentaje de mujeres de 35 a 39 años por número de hijos nacidos vivos.

 

Aquí podemos apreciar que el 20% de las mujeres de esta edad tiene 3 hijos y que estos porcentajes disminuyen para mujeres con menos de 3 hijos o más. Es claro que no es posible establecer una relación lineal entre el porcentaje de mujeres y su número de hijos, pues esto equivaldría a pretender que los puntos de la gráfica se encuentran cercanos a una recta.

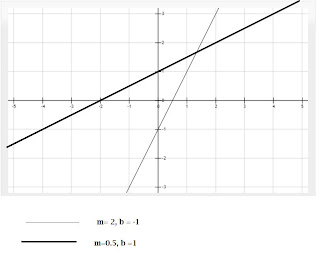
Una recta está determinada por una ecuación de la forma y = mx +b, donde m representa la pendiente y b la ordenada al origen. La pendiente nos indica el grado de inclinación de la recta y la ordenada al origen la altura del eje y por donde pasa la recta. En la primera de las siguientes figuras aparecen dos rectas con pendiente positiva y en la otra figura dos rectas con pendiente negativa.

Regresemos al problema de encontrar una recta que pase cerca de los ocho puntos (0, 88.5), (1.91.5),…, (7,106.3). Si variamos un poco la pendiente y la ordenada al origen podemos obtener una multitud de rectas semejantes  que pasen cerca de estos puntos. El criterio más usado para determinar una de estas rectas es el llamado método de mínimos cuadrados. Este método nos permite encontrar la recta que minimiza la suma de los cuadrados de las distancias verticales de la recta a los puntos.

Como ya observamos antes, para determinar esta recta es suficiente con establecer fórmulas para la pendiente y la ordenada al origen. Mediante el uso de técnicas de cálculo diferencial es posible deducir las siguientes formulas  para la pendiente y la ordenada al origen de la recta de mínimos cuadrados que pasa por los puntos ( $x_1 , y_1$ ), ($x_2 , y_2$), …,(x_n, y_n).
$m=\frac{n(\sum xy)-(\sum x)(\sum y))}{n\left [ \sum x^2-(\sum x)^2 \right ]}$ 
y
$b=\frac{(\sum y)\left [ \sum x^2 \right ]-(\sum x)(\sum xy)}{n\left [ \sum x^{2} \right ]-(\sum x)^{2}}    $

Aun cuando estas fórmulas parecen muy complicadas, es fácil emplearlas cuando el número de puntos no es muy grande, ya que las sumas requeridas para su aplicación se obtienen sin dificultad por medio de una tabla. Para el ejemplo de la productividad de los obreros en México que hemos venido estudiando la tabla es la siguiente.

En las dos primeras columnas escribimos los valores de los años y sus correspondientes productividades. En la tercera columna aparecen los cuadrados de la primera columna, y en la cuarta columna los productos de las dos primeras columnas. Es importante señalar que al emplearlas formulas debemos tener cuidado y no confundir los términos $\sum x^2$ y $(\sum_ x)^2$ que aparecen en el denominador. El primero de ellos es la suma de la tercera columna, y el segundo se obtiene al elevar al cuadrado la suma de la primera columna. Entonces,



$m=\frac{n(\sum xy)-(\sum x)(\sum y)}{n\left [ \sum x^2-(\sum x)^2 \right ]}$

=$\frac{8(2846.7)+(28)(782.3)}{8(140)-(28)^2}$
=$\frac{869.2}{336}=2.59$

Y
$b=\frac{(\sum y)\left [ \sum x^2 \right ]-(\sum x)(\sum xy)}{n\left [ \sum x^{2} \right ]-(\sum x)^{2}} $

=$\frac{(782.3)(140)-(28)(2846.7)}{8(140)-(28)^2}$
=$\frac{29814.4}{336}=88.7$




Observemos que si no hubiésemos identificado 1988 como 0, 1989 como 1,…, 1995 como 7, entonces los valores e la primera y tercer columnas hubieran sido muy grandes. Así, la recta de mínimos cuadrados viene dada por y =2.59 x +88.7. Podemos ahora utilizar esta ecuación para hacer predicciones. Las dos preguntas que motivaron este ejemplo eran: ¿cuándo esperamos que la productividad sea 25 % mayor que en 1993?y ¿cuál será la productividad en el año 2020?

En el caso de la primer pregunta conocemos el valor de y (la productividad, que es 125) y desconocemos el valor de x (el año). Debemos entonces despejar de la ecuación 125 = 2.59 x +88.7. Pasamos restando primero el 88.7 al lado izquierdo para obtener 125-88.7=36.3=2.59x, y ahora pasamos dividiendo el 2.59 para llegar a x =14.01. Esto significa que de continuar esta tendencia, 14 años después de 1988 (el año que corresponde al 0) la productividad será 125. Es decir en 2002, será un 25% superior con respecto a 1993.

En el caso de la segunda pregunta conocemos la x (el año) y desconocemos la y (la productividad), de modo que simplemente sustituimos el valor de x en la ecuación y = 2.59x +88.7 para obtener la productividad. Debemos antes ajustar el año 2020 con respecto a los valores de x, pero esto es sencillo pues basta restar 1988 a 2020 para obtener x, esto es , x =2020-1988 =32. Así, y = 2.59 (32)+88.7 =171.6. La productividad en 2020 será entonces aproximadamente 71.6 % más alta que en 1993.

Consideremos otro ejemplo. La población de México ha crecido considerablemente en los últimos años como podemos apreciar en la siguiente tabla.

Al identificar 1950 como 0, 1960 como 10,…,1995 como 45 y graficar tenemos la siguiente figura, donde en el eje de las x representamos los años y en el de las y las poblaciones.

Población de México en millones de habitantes

De la figura podemos ver que parece ser que si es razonable aproximar estos datos por una recta. Para aplicar las fórmulas debemos elaborar la siguiente tabla.

La pendiente y la ordenada al origen de la recta de minimos cuadrados están dadas por

$m=\frac{n(\sum xy)-(\sum x)(\sum y))}{n\left [ \sum x^2-(\sum x)^2 \right ]}$ 

=$\frac{6(10750)-(145)(349.9)}{6(5025)-(145)^2}$
=$\frac{13764.5}{9125}=1.51$
y
$b=\frac{(\sum y)\left [ \sum x^2 \right ]-(\sum x)(\sum xy)}{n\left [ \sum x^{2} \right ]-(\sum x)^{2}}$

$=\frac{(349.9)(5025)-(145)(10750)}{9125}$
$=\frac{199479.5}{9125}=21.9$

La recta de mínimos cuadrados es ahora y =1.51 x + 21.9. Podemos emplear esta ecuación para predecir cuándo tendrá México 130 millones de habitantes y cuál será la población del país en 2015. En el primer caso conocemos la y (la población que es 130), pero desconocemos la x (el año), esto es, tenemos la ecuación 130 = 1.51 x +21.9, de donde es fácil ver que x = 71.6. Este valor corresponde al año 1950 +71.6 = 2021.6. En el segundo caso simplemente sustituimos el valor de x =2015-1950=65 en la ecuación de la reta para tener que la población en 2015 será aproximadamente y =1.51 (65)+ 21.9 = 120 millones. Estos valores son estimaciones y deben tomarse con cierta reserva.